Yet Another Attempt at N-Body Simulations

If you know me, you know I love particle simulations. I've done countless attempts at making physics simulations in-browser before, but none have left me truly satisfied. The performance was always underwhelming by my standards, and I couldn't quite get multithreading down to scale it past ~200 bodies. A big part of this is due to the fact that I was using very inefficient O(N^2) algorithms for collision detection.

Recently, I discovered this video by William Y. Feng which talked about a data structure I hadn't heard before: The Quadtree.

By separating each particle into it's own quadrant, following a tree structure, we could instead calculate collisions in

O(N log N) since bodies calculating collision against bodies outside of it's own node, can use an external node's approximated mass (summed average of all it's children) instead of calculating against every single other particle. This does lead to a small tradeoff in accuracy, however this is entirely negligible for this application.

How does it work?

First, it's important to see what's going on visually. We start with a single root node the size of our simulation, and that node is subdivided into four quadrants. Say we add 2 bodies in the top left quadrant, that quadrant will be subdivided into four quadrants again, and those bodies will occupy their respective node related to their quadrant. Let's take a look at figure 1:

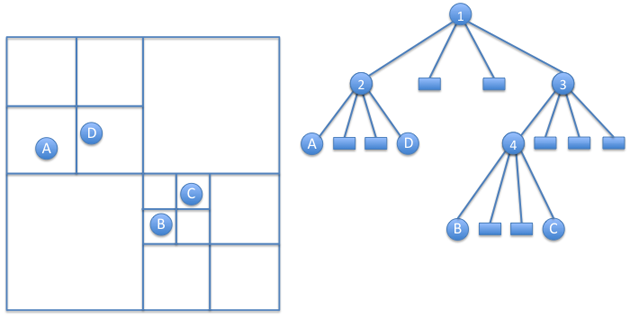
In this example, the quadtree begins at the NW quadrant, or the first subdivision. We'll call it by it's node number, Node 2. Node 2 contains more than 1 particle, so it is again subdivided into four quadrants. A and D will occupy Node 2's SW quadrant and SE quadrant respectively. They become the parent body for their node. Say we were to add another body in Node 2's SW quadrant (e.g. body E), the quadrant will be subdivided into four more quadrants.

During any subdivision, the body that occupied the node will be pushed down to it's respective quadrant, and the 2nd body that caused the subdivision as well.

The code

First, the Body class. Each body contains it's position, velocity, mass, radius, and heat. Here, I'm using verlet integration, so we use nextPos and nextVel to determine how the body will move in the next step.

class Body {
  pos: Vector;
  vel: Vector;
  mass: number;
  radius: number;
  nextPos: Vector;
  nextVel: Vector;
  heat: number;

  constructor(
    pos: Vector,
    vel: Vector,
    mass: number,
    radius: number,
    heat: number
  ) {
    this.pos = pos;
    this.nextPos = pos.copy();
    this.nextVel = vel.copy();
    this.vel = vel;
    this.mass = mass;
    this.radius = radius;
    this.heat = heat;
  }

  update(dt: number) {
    this.vel.mult(dt);
    this.pos.add(this.vel);
    this.heat *= 0.997; // time lowers heat
  }
}

Next, the TreeNode class. I named this class TreeNode instead of Quadtree because it's easier to understand the tree as a graph of nodes. We'll separate the code in steps to make it easier to understand. The complete code for the Quadtree/TreeNode class can be found

here

this class contains a couple properties:

• x: The x position of the node
• y: The y position of the node
• w: The width of the node
• children: The list of children of the node
• leaf: Whether the node is a leaf or not (A leaf in a quadtree is a node that does not have any child nodes (subdivisions), and it either contains a single body or no body at all)
• body: The body of the node if it's a leaf, or null if it's subdivided (contains 2 or more bodies)
• totalCenter: The gravitational center of mass of the node.
• center: The center vector (x, y coordinates) of the node
• totalMass: The total mass of the node
• count: The number of bodies in the node

class TreeNode {
  x: number;
  y: number;
  w: number;
  children: TreeNode[];
  leaf: boolean;
  body: Body | null;

  totalCenter: Vector; // "Total" center of mass
  center: Vector | null;
  totalMass: number;
  count: number; // Number of bodies in this node

  constructor(
    pos: Vector,
    vel: Vector,
    mass: number,
    radius: number,
    heat: number
  ) {
    this.pos = pos;
    this.nextPos = pos.copy();
    this.nextVel = vel.copy();
    this.vel = vel;
    this.mass = mass;
    this.radius = radius;
    this.heat = heat;
  }
}

Whenever a node is subdivided, we'll split it into 4 new quandrants/nodes.

split() {
  const newWidth = this.w * 0.5;
  this.children[0] = new TreeNode(this.x, this.y, newWidth); // nw
  this.children[1] = new TreeNode(this.x + newWidth, this.y, newWidth); // ne
  this.children[2] = new TreeNode(this.x, this.y + newWidth, newWidth); // sw
  this.children[3] = new TreeNode(this.x + newWidth, this.y + newWidth, newWidth); // se
  this.leaf = false; // It has been subdivided, so it's no longer a leaf
}

Next is the which() function, which returns the quadrant that the body should be added to.

which(v: Vector): number {
  const halfWidth = this.w * 0.5;
  if (v.y < this.y + halfWidth) {
    return v.x < this.x + halfWidth ? 0 : 1;
  }

  return v.x < this.x + halfWidth ? 2 : 3;
}

Next is the insert() function, which inserts a body into the tree. We'll break this down into steps to make it easier to understand. First, we must determine if this node is a leaf.

If it is not a leaf, insert the new body into the correct quadrant (calculated using the which() function).

insert(newBody: Body) {
  ...

  // If it's not a leaf, insert new body into this node
  this.totalCenter.add(newBody.pos);
  this.totalMass += newBody.mass;
  this.count++;
  this.children[this.which(newBody.pos)].insert(newBody);
}

If it's a leaf and does not contain a body, this is very simple. We just add the body and adjust the total center and mass. Don't forget to up the count.

insert(newBody: Body) {
    if (this.leaf) {
      // If it does not already contain a body, add it and adjust total center and mass
      if (!this.body) {
        this.body = newBody;
        this.totalCenter.add(newBody.pos);
        this.totalMass += newBody.mass;
        this.count++;
        return;
      }

      ...
    }
    ...
}

If the node already contains a body, the process becomes a bit more complex. First, we need to:

1. Recalculate the total center of mass and the total mass of the node by accounting for the new body.
2. Increase the body count in the node.

Next, we determine which quadrants the bodies should be placed in using the which() function. The first body (a) will go into quadrant qA, and the second body (b) will go into quadrant qB.

In cases where the two bodies are very close to each other, we use a while loop to keep subdividing the node until the bodies are separated into different quadrants.

insert(newBody: Body) {
    if (this.leaf) {
      if (!this.body) {
        ... // Previous example
      }

      // If it contains a body, split and insert the current & new body into their individual nodes
      const a = this.body;
      const b = newBody;

      this.totalCenter.add(b.pos);
      this.totalMass += b.mass;
      this.count++;

      let cur = this as TreeNode;
      let qA = cur.which(a.pos);
      let qB = cur.which(b.pos);

      while (qA == qB) {
        // Current node becomes a's qudrant, splits, and qA & qB get recalculated
        cur.split();
        cur = cur.children[qA];
        qA = cur.which(a.pos);
        qB = cur.which(b.pos);

        // Update total center and mass of new current node
        cur.totalCenter.add(a.pos);
        cur.totalCenter.add(b.pos);
        cur.totalMass += a.mass + b.mass;
        cur.count += 2;
      }

      cur.split();
      cur.children[qA].body = a;
      cur.children[qB].body = b;

      // Update center of mass and total for lowest-level child
      cur.children[qA].totalCenter.add(a.pos);
      cur.children[qB].totalCenter.add(b.pos);
      cur.children[qA].totalMass += a.mass;
      cur.children[qB].totalMass += b.mass;
      cur.children[qA].count++;
      cur.children[qB].count++;


      // this node becomes a parent node, so it no longer has an associated body
      this.body = null;
      return;
    }
}

Gravity

// Acceleration due to the gravity exerted by a on b
function gravityAcc(a: Vector, b: Body, dt: number) {
  const distSq = distSquared(a, b.pos);

  if (distSq <= 2 * (b.radius * b.radius)) {
    // To verify if 2* is good
    return new Vector(0, 0);
  }

  // Acceleration due to gravity
  // aGrav = ((a - b.pos) * deltaT * G * b.mass ) / (distSq * sqrt(distSq))
  return Vector.getMult(
    Vector.getSub(a, b.pos),
    (dt * G * b.mass) / (distSq * Math.sqrt(distSq))
  );
}

export function gravity(bodies: Body[], root: TreeNode, dt: number) {
  bodies.forEach((b) => {
    gravitate(b, root, dt);
  });
}

function gravitate(b: Body, tn: TreeNode, dt: number) {
  // If the tree node is a leaf, then it represents a single body
  if (tn.leaf) {
    // If the body doesn't exist or is the same as the current body, then there's no gravity to apply
    if (!tn.body || b == tn.body) return;

    // Otherwise, add the acceleration due to the gravity of the body to the current body
    b.vel.add(gravityAcc(tn.body.pos, b, dt));
    return;
  }

  // If the tree node is not a leaf, then it represents a collection of bodies
  // Get the center of mass of the collection
  if (!tn.center) {
    tn.center = Vector.getMult(tn.totalCenter, 1.0 / tn.count);
  }

  // If the collection is far enough away, then treat it as a single body
  if (tn.w / dist(b.pos, tn.center) < theta) {
    // Calculate the acceleration due to the collection's gravity
    b.vel.add(gravityAcc(tn.center, b, tn.totalMass));
    return;
  }

  // If the collection is close enough, then recursively calculate the gravity of each child
  tn.children.forEach((child) => gravitate(b, child, dt));
}